This unit introduces foundational algebraic concepts‚ focusing on linear equations‚ inequalities‚ and systems. It emphasizes problem-solving and mathematical modeling‚ preparing students for advanced algebraic reasoning. The answer key provides detailed solutions‚ aiding in self-assessment and deeper understanding of the material.
1.1 Overview of the Unit
Illustrative Mathematics Algebra 1 Unit 2 focuses on linear equations‚ inequalities‚ and systems. It builds foundational skills in solving equations‚ graphing‚ and modeling real-world problems. The unit emphasizes understanding constraints and relationships‚ preparing students for advanced algebraic concepts. The answer key provides step-by-step solutions‚ enabling students to verify their work and grasp complex mathematical ideas effectively.
1.2 Importance of the Answer Key
The answer key is an essential resource for students and educators‚ offering detailed solutions to exercises and assessments. It aids in self-assessment‚ clarifies complex concepts‚ and reinforces learning by providing step-by-step explanations. This tool ensures understanding and preparedness for future units‚ aligning with the curriculum’s focus on linear equations‚ inequalities‚ and systems in Illustrative Mathematics Algebra 1 Unit 2.

Structure of the Answer Key
The answer key is organized as a PDF document‚ providing clear solutions to exercises and assessments. It aligns with unit content‚ ensuring accurate understanding and preparation.
2.1 Organization of the PDF Document
The answer key is structured as a PDF document‚ divided into clear sections corresponding to each lesson and topic within Unit 2. It includes detailed solutions to practice problems‚ assessments‚ and exercises‚ ensuring alignment with the unit’s content. The document is formatted for easy navigation‚ with headings‚ bullet points‚ and numbered lists to enhance readability and quick access to specific answers.
2.2 Key Features of the Answer Key
The answer key provides detailed solutions to all practice problems‚ assessments‚ and exercises in Unit 2. It includes step-by-step explanations for complex questions‚ ensuring clarity and understanding. The document is aligned with the unit’s content‚ covering linear equations‚ inequalities‚ and systems. Clear formatting‚ including headings and bullet points‚ enhances readability. It serves as a valuable resource for students to verify their work and understand their mistakes.
Linear Equations and Inequalities
Linear equations and inequalities form the foundation of algebraic problem-solving. They involve variables‚ constants‚ and basic operations‚ with inequalities introducing concepts like “less than” or “greater than.” These tools model real-world situations‚ from budgeting to scientific calculations‚ emphasizing critical thinking and practical application.
3.1 Solving Linear Equations

Solving linear equations involves isolating the variable using inverse operations. Steps include simplifying both sides‚ combining like terms‚ and performing operations to solve for the variable. The answer key provides step-by-step solutions‚ ensuring understanding of equation manipulation. Mastery of this skill is essential for modeling real-world problems and progressing in algebraic studies. Practice worksheets and video resources support independent learning and skill reinforcement.
3.2 Understanding Linear Inequalities
Linear inequalities introduce the concept of expressions with an inequality symbol (<‚ >‚ ≤‚ ≥). Solving involves similar steps to equations‚ with careful consideration when multiplying or dividing by negative numbers. Graphing solutions on a number line helps visualize the range of valid answers. Real-world applications‚ such as budget constraints‚ demonstrate the practical relevance of inequalities. The answer key provides clear solutions‚ aiding in understanding and mastery of this essential algebraic skill.
Systems of Linear Equations
Systems of linear equations involve two or more equations with variables. Solutions are coordinate pairs making all equations true. Graphical solutions show intersections‚ while algebraic methods like substitution or elimination provide precise answers. Real-world applications highlight the practical relevance of solving systems‚ ensuring students grasp their importance in modeling real-life scenarios.
4.1 Graphical Solutions
Graphical solutions involve plotting systems of linear equations on a coordinate plane. The point where the lines intersect represents the solution. This method provides a visual interpretation‚ helping students understand how equations relate. Sketching the lines and identifying the intersection point allows for an intuitive approach to solving systems. However‚ graphical methods may lack precision for complex systems‚ making algebraic techniques more reliable in such cases.
4.2 Algebraic Methods
Algebraic methods‚ such as substitution and elimination‚ provide precise solutions to systems of linear equations. These techniques involve manipulating equations to solve for variables. Substitution entails solving one equation for a variable and substituting it into the other. Elimination uses combining equations to eliminate a variable. Both methods are efficient and reliable‚ offering exact solutions compared to graphical approaches‚ and are essential for solving complex systems accurately.

Graphing Linear Equations
Graphing linear equations involves plotting points on a coordinate plane to visualize solutions. This method helps identify patterns and understand relationships between variables‚ aiding in verifying solutions using the answer key.
5.1 Identifying Slope and Intercept
Identifying slope and intercept is crucial for graphing linear equations. The slope determines the steepness‚ while the intercept is the y-axis crossing point. Using the answer key‚ students verify calculations and understand how these elements define the line’s direction and position‚ enhancing their ability to plot equations accurately and interpret their graphical representations effectively.

5.2 Plotting Points on a Coordinate Plane
Plotting points on a coordinate plane involves identifying the x and y coordinates. The answer key provides clear examples‚ showing how to locate points accurately. It emphasizes understanding the axes and quadrants‚ ensuring precise placement. This skill is fundamental for graphing equations and interpreting their visual representations effectively.

Modeling with Equations
Modeling with equations involves translating words into mathematical expressions. This unit teaches students to represent real-world scenarios algebraically‚ enabling them to analyze and solve practical problems effectively.
6.1 Translating Words into Mathematical Expressions
Translating words into mathematical expressions is a core skill in algebra. Students learn to identify variables‚ constants‚ and operations hidden in verbal descriptions. For instance‚ “5 more than x” becomes x + 5. The answer key provides examples and step-by-step solutions‚ helping students master this fundamental process. This skill is essential for modeling real-world problems and solving them algebraically with confidence.
6.2 Real-World Applications
Algebraic concepts are applied to real-life scenarios‚ such as budgeting‚ resource allocation‚ and financial planning. Students learn to model situations like grocery spending limited by income and other practical constraints. The answer key offers clear solutions and examples‚ helping students grasp the practical uses of equations and inequalities‚ thereby enhancing their ability to solve everyday problems mathematically with confidence and accuracy.

Constraints and Solutions
Constraints define boundaries for solutions‚ guiding problem-solving in real-world contexts like budgeting or resource allocation. Analyzing constraints helps identify valid solutions within defined limits‚ ensuring practical applications of inequalities and equations.
7.1 Analyzing Constraints
Analyzing constraints involves identifying and interpreting limitations or boundaries within mathematical problems. Constraints help define the range of possible solutions‚ ensuring they align with real-world contexts. In Algebra 1 Unit 2‚ students learn to translate these constraints into inequalities or equations‚ applying them to scenarios like budgeting or resource allocation. This skill is essential for modeling practical problems and interpreting solutions accurately.
7.2 Finding Valid Solutions
Finding valid solutions involves identifying values that satisfy all given constraints and equations. In Unit 2‚ students learn to verify solutions by substituting them back into original problems. This ensures accuracy and relevance‚ particularly in real-world applications. The answer key provides step-by-step validations‚ helping students understand how to confirm their answers align with problem constraints and achieve practical‚ meaningful results.
Extra Support Materials
Extra support materials include practice worksheets and video resources‚ offering additional guidance for mastering linear equations‚ inequalities‚ and systems. These tools align with the answer key‚ enhancing understanding and problem-solving skills effectively.
8.1 Practice Worksheets
Practice worksheets provide targeted exercises for mastering concepts like solving linear equations‚ graphing‚ and modeling real-world scenarios. They align with the answer key‚ offering step-by-step solutions and explanations. These resources help students reinforce learning‚ identify areas for improvement‚ and build confidence in their algebraic skills through structured and varied practice opportunities.
8.2 Video Resources
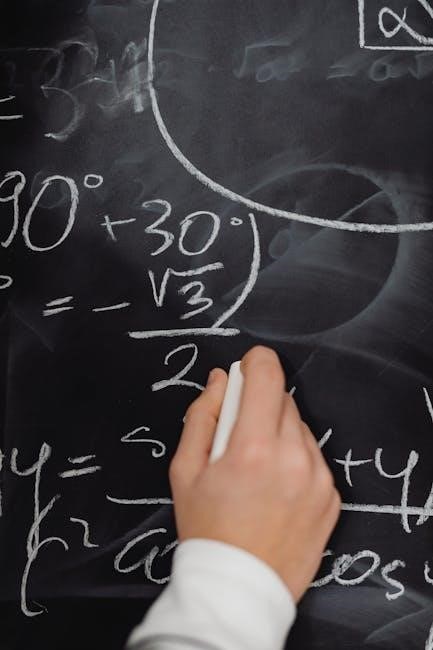
Video resources complement the answer key by providing visual explanations and step-by-step solutions for complex problems. They cover topics like solving linear equations and graphing inequalities‚ offering detailed walkthroughs. These videos support visual learners and reinforce concepts discussed in the unit‚ helping students grasp difficult ideas through engaging‚ interactive explanations.
Unit Assessments
Unit assessments evaluate student understanding of algebraic concepts‚ ensuring mastery of linear equations‚ inequalities‚ and systems. They include formative and summative evaluations to measure progress effectively.
9.1 Formative Assessments
Formative assessments monitor student progress throughout the unit‚ using quizzes‚ class discussions‚ and homework checks. These evaluations identify gaps in understanding and guide instructional adjustments. The answer key supports immediate feedback‚ enabling students to correct mistakes and reinforce learning. Regular check-ins ensure students grasp key concepts before moving to more complex material‚ fostering a strong foundation in algebraic principles.
9.2 Summative Assessments
Summative assessments evaluate student mastery at the unit’s end‚ typically through comprehensive tests or projects. These assessments measure understanding of linear equations‚ inequalities‚ and systems. The answer key provides accurate solutions‚ allowing students to review their work and identify areas for improvement. Summative assessments ensure readiness for future units and reinforce the application of algebraic concepts to real-world problems.
Teacher Guide for Unit 2
The teacher guide provides detailed lesson plans and classroom activities for Unit 2‚ supporting educators in delivering effective instruction. It includes resources for differentiation and assessment‚ ensuring comprehensive coverage of algebraic concepts and student engagement. Additional support materials are also available to enhance teaching strategies and student understanding.

10.1 Lesson Plans
The lesson plans for Unit 2 are detailed and structured to ensure comprehensive coverage of algebraic concepts. They include step-by-step instructions for teaching linear equations‚ inequalities‚ and systems‚ with embedded formative assessments. Each lesson incorporates collaborative activities‚ problem-solving tasks‚ and opportunities for students to articulate their reasoning. Additional resources‚ such as worksheets and video links‚ are provided to support differentiated instruction and enhance student engagement. The plans emphasize conceptual understanding and procedural fluency‚ aligning with the unit’s learning objectives. Teachers can adapt the plans to meet the diverse needs of their students while maintaining the integrity of the curriculum. The lesson plans also include suggestions for integrating real-world applications‚ making the content relevant and meaningful for learners. This ensures that students develop a strong foundation in algebra‚ preparing them for future units and advanced mathematical studies. The clarity and organization of the lesson plans make them an invaluable tool for educators aiming to deliver effective and impactful instruction. By following the lesson plans‚ teachers can foster a deeper appreciation of mathematics and cultivate critical thinking skills in their students. Overall‚ the lesson plans for Unit 2 are designed to promote academic success and long-term mathematical proficiency. They provide a balanced approach to teaching‚ combining theoretical knowledge with practical application‚ ensuring that students are well-prepared for the challenges of algebra. The lesson plans are regularly updated to reflect best practices in mathematics education‚ ensuring that they remain relevant and effective in supporting student learning. Through these plans‚ teachers can create an inclusive and supportive learning environment that encourages active participation and intellectual growth. The lesson plans are an essential component of the unit‚ guiding teachers in their efforts to inspire and educate the next generation of mathematicians and problem solvers. They serve as a roadmap for achieving the unit’s goals‚ ensuring that all students have the opportunity to succeed and thrive in their mathematical journey. The lesson plans are comprehensive‚ flexible‚ and aligned with the principles of Illustrative Mathematics‚ making them a trusted resource for educators. By adhering to these plans‚ teachers can confidently deliver high-quality instruction that meets the needs of all learners. The lesson plans for Unit 2 are a testament to the commitment of Illustrative Mathematics to excellence in mathematics education‚ providing teachers with the tools they need to make a positive impact on their students’ academic lives. They are a vital part of the educational process‚ helping to shape the mathematical understanding and skills of future generations. The lesson plans are more than just a guide; they are a pathway to mathematical mastery‚ empowering teachers to inspire‚ motivate‚ and educate their students effectively. They embody the core values of Illustrative Mathematics‚ prioritizing depth over breadth and fostering a love of learning that extends beyond the classroom. The lesson plans for Unit 2 are a valuable resource that supports teachers in their mission to provide exceptional mathematics education. They are a key factor in helping students achieve their full potential and succeed in an increasingly complex and mathematically driven world. The lesson plans are a cornerstone of the unit‚ offering a structured and supportive framework for teaching and learning. They are designed to help teachers create a positive and productive learning environment where students can explore‚ discover‚ and master the principles of algebra. The lesson plans are a reflection of the dedication of Illustrative Mathematics to improving mathematics education and preparing students for future challenges. They are a comprehensive and dynamic resource that evolves with the needs of educators and students‚ ensuring that the teaching of algebra remains engaging and effective. The lesson plans for Unit 2 are a fundamental part of the educational experience‚ providing teachers with the guidance and resources they need to help students excel in mathematics. They are a celebration of the power of education to transform lives and a commitment to excellence in teaching and learning. The lesson plans are a shining example of how well-structured and thoughtful curriculum design can make a profound difference in the quality of education. They are a source of inspiration and empowerment for teachers‚ enabling them to make a lasting impact on their students’ mathematical understanding. The lesson plans for Unit 2 are a testament to the enduring importance of mathematics in shaping the minds of future generations. They are a powerful tool in the hands of educators‚ helping to unlock the potential of every student and nurture a lifelong love of learning. The lesson plans are a cornerstone of the unit’s success‚ providing a clear and effective pathway for teaching and learning. They are a valuable asset for teachers‚ offering the support and guidance needed to deliver high-quality instruction. The lesson plans for Unit 2 are a vital component of the educational process‚ ensuring that students receive the best possible start in their mathematical journey. They are a celebration of the transformative power of education and a commitment to helping students achieve their full potential. The lesson plans are a key element in the pursuit of excellence in mathematics education‚ offering teachers the resources and strategies they need to inspire and educate their students. They are a testament to the importance of thoughtful curriculum design in fostering academic success and a love of learning. The lesson plans for Unit 2 are a comprehensive and dynamic resource that supports teachers in their mission to provide exceptional mathematics education. They are a pathway to mathematical mastery‚ empowering students with the knowledge‚ skills‚ and confidence they need to succeed in an ever-changing world. The lesson plans are a shining example of how well-designed educational resources can make a meaningful difference in the lives of students and teachers alike. They are a celebration of the power of education to transform lives and a commitment to excellence in teaching and learning. The lesson plans for Unit 2 are a fundamental part of the educational experience‚ providing teachers with the tools they need to help students excel in mathematics. They are a source of inspiration and empowerment for educators‚ enabling them to make a lasting impact on their students’ mathematical understanding. The lesson plans are a cornerstone of the unit’s success‚ offering a structured and supportive framework for teaching and learning. They are a vital resource for teachers‚ ensuring that they can deliver high-quality instruction that meets the needs of all learners. The lesson plans for Unit 2 are a testament to the enduring importance of mathematics in shaping the minds of future generations. They are a powerful tool in the hands of educators‚ helping to unlock the potential of every student and nurture a lifelong love of learning. The lesson plans are a key element in the pursuit of excellence in mathematics education‚ offering teachers the resources and strategies they need to inspire and educate their students. They are a celebration of the transformative power of education and a commitment to helping students achieve their full potential. The lesson plans for Unit 2 are a comprehensive and dynamic resource that supports teachers in their mission to provide exceptional mathematics education. They are a pathway to mathematical mastery‚ empowering students with the knowledge‚ skills‚ and confidence they need to succeed in an ever-changing world. The lesson plans are a shining example of how well-designed educational resources can make a meaningful difference in the lives of students and teachers alike. They are a testament to the importance of thoughtful curriculum design in fostering academic success and a love of learning. The lesson plans for Unit 2 are a fundamental part of the educational process‚ ensuring that students receive the best possible start in their mathematical journey. They are a source of inspiration and empowerment for teachers‚ enabling them to make a lasting impact on their students’ mathematical understanding. The lesson plans are a cornerstone of the unit’s success‚ offering a clear and effective pathway for teaching and learning. They are a valuable asset for educators‚ providing the support and guidance needed to deliver high-quality instruction. The lesson plans for Unit 2 are a vital component of the educational experience‚ helping to shape the mathematical understanding and skills of future generations. They are a powerful tool in the hands of teachers‚ enabling them to inspire‚ motivate‚ and educate their students effectively. The lesson plans are a key element in the pursuit of excellence in mathematics education‚ offering the resources and strategies necessary to foster academic success. They are a testament to the transformative power of education and a commitment to helping students achieve their full potential. The lesson plans for Unit 2 are a comprehensive and dynamic resource that supports teachers in their mission to provide exceptional mathematics education. They are a pathway to mathematical mastery‚ empowering students with the knowledge‚ skills‚ and confidence they need to succeed in an ever-changing world. The lesson plans are a shining example of how well-designed educational resources can make a meaningful difference in the lives of students and teachers alike. They are a celebration of the power of education to transform lives and a commitment to excellence in teaching and learning. The lesson plans for Unit 2 are a fundamental part of the educational experience‚ providing teachers with the tools they need to help students excel in mathematics. They are
10.2 Classroom Activities
Classroom activities for Unit 2 are designed to engage students in active learning. Collaborative problem-solving tasks encourage peer discussion and teamwork. Graphing exercises and real-world application scenarios help students connect abstract concepts to practical situations. Differentiated instruction strategies‚ such as group work and technology integration‚ cater to diverse learning needs. Hands-on activities‚ like creating models of linear equations‚ reinforce understanding and promote retention of key concepts. These activities foster critical thinking and mathematical fluency‚ ensuring students are well-prepared for assessments and future units.



0 Comments